In the opening vignette, Melissa (the first author) listened to how children talked about their learning with a peer. The use of language is a powerful way for children to engage in their own thinking and the thinking of their classmates. Early childhood settings should be environments rich with opportunities that promote social, linguistic, and cognitive development (NAEYC 2020). One way to achieve this is by creating meaningful social contexts in which children actively engage with their peers (Bedrova and Leong 2015; Park and Lee 2015; Zippert et al. 2019).

As a group of researchers from the University of Texas San Antonio, we (the authors) embarked on a 10-week qualitative research study of children in paired learning situations. Specifically, we asked: What influence does working in pairs have on young children’s approaches to problem solving and their ability to verbalize and communicate a pattern to a partner? To address this question, we focused on one dual language prekindergarten classroom with 24 predominantly Latino/a, working-class families of Mexican descent in an urban private Catholic school. All 24 prekindergarten children had varying levels of Spanish and English bilingualism; however, most were native English speakers acquiring Spanish as a heritage language. We chose this campus because the teachers used a partner-based strategy for learning as a requirement in their two-way dual language program. We spent time specifically observing the interactions between two pairs of children working in the math center on patterning concepts.

Because patterns are basic to the understanding of mathematical concepts (Zippert, Douglas, & Rittle-Johnson 2020; Wijns et al. 2021), we focused on children’s math skills of recognizing, extending, and abstracting patterns with a partner. In this article, we provide a brief literature review on the significance of partner work for young children’s linguistic and academic development. We include the strategies we used to scaffold children’s mathematical understanding, and we present descriptions of three themes that emerged from an analysis of our observational data related to how children expressed their mathematical understanding:

• drawings
• physical movement
• representation through concrete materials

Although our work focused on children in dual language classrooms, we conclude by offering implications for early childhood teachers in a variety of classroom settings.

What We Know About Partner Work for Young Children

According to sociocultural theory (Vygotsky 1978), children’s mental, linguistic, and social development is spurred by more competent others through social interactions. These more competent others are also referred to as more knowledgeable others. Vygotsky’s theory focuses heavily on the role of social context in the construction of knowledge—an interaction that creates space for children to exchange ideas and learn from each other’s perspectives. This often pushes learners to reorganize and restructure their thinking, leading to higher levels of understanding.

Learning in peer-based interactions has been tied to greater conceptual understanding and language development across subject areas such as mathematics, reading, and science (Alanís 2018; Zippert et al. 2019). The success of the pairings, however, often depends on how the teacher has structured collaborative tasks and how children interact during their partner-based work (Alanís 2018; Arreguín-Anderson & Alanís 2019; Gkloumpou & Germanos 2022). For example, when intentionally paired with a more socially knowledgeable peer, children in one study showed improvements on a perspective-taking task and had higher learning scores on a classification task when they worked together (Park & Lee 2015). The way children engaged with each other influenced their motivation and persistence for the tasks as well as self-perceptions.

Within the context of math, partner learning has shown specific benefits. Math talk with a peer promotes a mathematician identity in which all learners have access to math understanding and can express that understanding in empowering ways (Fuson, Clements, & Sarama 2015). Partner work gives children an opportunity to be heard and to try out math ideas that they may then feel comfortable sharing within a larger group (Zippert, Douglas, & Rittle-Johnson 2020). In addition, preschoolers who worked on mathematical concepts in cooperative settings showed improvements in their listening skills and in their awareness of others (Zippert et al. 2019).

Scaffolding Mathematical Experiences for Children

For this study, we engaged with children while they were learning with pairs at their math center during daily center time. These pairings had already been determined by the classroom teacher, and partner-based activities such as reading and writing with a partner, exploring artifacts with a partner, and completing rhyming activities with a partner were routinely implemented. The classroom teacher used a heterogeneous partnering of children based on their English language levels and their understanding of mathematical concepts to facilitate a zone of proximal development (ZPD). This ZPD allows for children to work with more knowledgeable others so that they work at a level just beyond what they can do independently.

Children had worked in pairs since the beginning of the school year. Now in February, they were used to traveling with their partners to a center of their choice and engaging in various partner-based activities. Although children were given the option of working by themselves, they seemed to prefer to engage with a peer. We often heard them say, “Come on partner. Let’s go to another center,” or introduce themselves and their partner to us with, “This is Luis. He’s my partner.”

To further our inquiry about the relationship between partner-based work and mathematical understanding, we created several pattern and sorting experiences using manipulatives such as drawing and extending patterns for children to engage in with their partners. To facilitate the learning process, Melissa modeled for children several strategies to scaffold interactions and language use, such as the use of questions and sentence stems or frames.

Questioning helped children stretch their learning to a deeper level and augment their math skills (Spreckelsen et al. 2019). Melissa first modeled how children could use questioning to clarify ideas. For example, she asked questions such as

• Can you explain it to her?
• Why do you think that?
• Can you sort that again in another way?
• What could your partner do to fix their pattern?

She then encouraged children to use those questions with their peers.

Next, we adapted sentence stems from work by Chapin and O’Connor (2013) that could be used to extend conversations, increase interactions, and promote mathematical language. Sentence stems or frames can help children who are learning content in their second or third language organize their thoughts while also extending their thinking (Arreguín-Anderson & Alanís 2019). These stems encouraged the children to increase their overall language development, justify answers, and engage in each other’s thinking. We focused on the following sentence frames:

• Can you make it a different way?
• Tell me what you are thinking.
• Describe your drawing or pattern.
• What do you think I am going to put next?

The pairs were encouraged to use this language to engage with each other and explain their mathematical thinking.

Partner-Based Patterning Activities

---

The math center activities we created focused on growing in pattern understanding. This content is the foundation for later algebraic reasoning (see “Promoting Algebraic Reasoning in the Early Years” by Lindsey Perry for more on this topic); therefore, time is well spent in early childhood settings fostering this awareness (Zippert et al. 2019). For many young learners, sorting is a precursor to more abstract pattern understanding (Reed & Mercer Young 2017). Hence, we provided a bucket of objects, including shells, tiles, and rocks so children could practice their sorting skills as they progressed to more challenging pattern formations.

We used additional scaffolding strategies for all of the children, including placing photographs in the math center of patterns found in nature. We asked children to find the patterns around them, such as light shining through the window blinds and tiles on the floor. This led to pattern scavenger hunts in the classroom where pairs of children located multiple patterns within their classroom. They shared their findings with their partners upon returning to the math center. We heard children excitedly saying, “We found a pattern!” or “Look at our patterns!” These types of activities provided a space where children could stretch their understanding to include more abstract thinking and mathematical connections to their everyday surroundings.

We also developed center-based activities that exposed children to different types of patterns (AB, ABBA, AABB, ABC). Children were given patterns and asked to work with their partners to name the type of pattern, extend it, and then create the pattern using other materials. They recognized the four different types of patterns through extending and duplicating them in interactive pair-based activities. The following sections describe each of the three ways children expressed their mathematical understanding of patterns when engaging with their peers.

Ways of Showing and Scaffolding Understanding with a Partner

Children learn mathematics by engaging with it in as many ways as possible (Kibbe & Feigenson 2017). We observed children use different ways to scaffold each other’s understanding. These included drawings, physical movement, and manipulatives. Each of these strategies led to deeper engagement with patterns and new ways to express their mathematical thinking through visual, physical, and verbal responses.

“I Drew the Shell Blue, Red, Blue, Red”

---

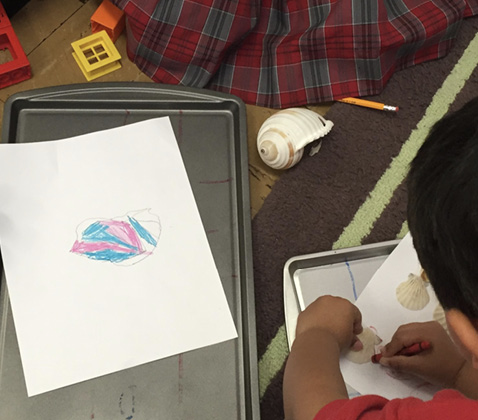
While Vygotsky (1978) stressed the importance of language in learning environments, drawings can also serve as a tool to enhance children’s thoughts and understanding. This bridge can help children internalize their thinking because drawing becomes the tool they use to express that thinking. This is particularly helpful for multilingual learners whose oral language skills in English may prevent them from sharing their understanding with their English-speaking partners. Drawings provide a common point of reference to see new knowledge on paper. They also serve as a powerful product of children’s learning and a significant way to share their understanding (Kim & Kim 2017). For Cara and Joseph, their drawing dialogues led to deeper meaning making and shared learning because they were able to show and explain to each other how they had created patterns and how those patterns could be augmented. Drawings can also become valuable in authentic learning portfolios where children can see threads of their thinking progress over time and teachers can assess their levels of understanding.

“We Can Make Patterns with Our Hands and Feet”

Young children are multimodal learners. They use language to communicate, but they also use gestures, visuals, and sounds (Arreguín-Anderson & Alanís 2019). In the following dialogue example, children’s growth in understanding patterns can be seen in their ability to create a pattern in a new way. Here, Melissa uses movement and rhythmic clapping to develop Monica’s understanding of patterns. The use of movement and clapping is developmentally appropriate in the early childhood classroom because it taps into children’s developmental need for concrete representations, allows for multimodal learning, and engages children in playful activity (NAEYC 2020).

---

In this interaction, children communicated their pattern with movement and then matched their pattern with concrete materials such as beads and stickers. This was particularly beneficial for Monica, who was still developing her English skills, because she could visually see and act out the pattern without relying on English. We observed that Monica was more interested in movement patterns and could duplicate Stephanie’s patterns through movement more consistently than when she was only using manipulatives. Teacher-created pairings revealed Stephanie was the more knowledgeable other in her math understanding. Monica, however, grew in her pattern understanding through her own chosen modality of movement. In a subsequent interaction with Monica, the following communication took place.

---

The ability to engage in a conversation about the types of patterns she was creating provided a space for Monica to use her new vocabulary along with movement to show her mathematical understanding to Stephanie. It also revealed Monica’s ability to mathematize through the modality of movement.

“Diamond, Circle, Diamond, Circle, Triangle . . . Oops!”

Manipulatives are a staple in most early childhood math centers. They offer concrete ways for children to make meaning of abstract mathematical concepts. Manipulatives are especially important for young multimodal learners because children can see and hold them. This helps the children attach labels to real objects and makes learning concrete.

One afternoon, Diego and Alicia were engaged in drawing AB patterns with shapes. As Diego created a pattern, he asked Alicia to look at what he had done.

---

Saying the pattern aloud to Alicia helped Diego adjust and accommodate his understanding immediately. This might not have happened if Diego had been working alone.

In this study, children explored repeating patterns with rocks, leaves, shells, tiles, beads, stickers, interlocking cubes, and pompoms. Similar to Monica’s choice in using movement to represent her understanding, children’s choice of materials was an effective way to increase engagement with math patterns. They most often created patterns together and for each other using a variety of materials. During this interactive process, children used math vocabulary such as AB pattern and mathematical dialogue to explain why they created a certain pattern. They also learned from their errors when the pattern did not make sense. Children became very capable of switching among objects, such as creating a pattern with beads, then showing that same type of pattern to their partners with interlocking cubes and stickers.

We were fascinated when children would create a pattern and then cover part of it to see if their partner could guess the concealed part. This type of abstraction in patterning increases flexible thinking and encourages children to use their own ideas to represent the pattern in a new way (Zippert, Douglas, & Rittle-Johnson 2020). These situations offer a rich context for children to develop confidence in their mathematical abilities.

Addressing Different Levels of Engagement

Like Park and Lee (2015), we took particular note of how children engaged at the math center for longer periods of time than they had prior to our research study. We also noticed how they often negotiated each other’s interests and ideas instead of moving on to something else. However, the statement, “I want to do something else now” was heard a few times.

Inevitably, young learners will have different levels of engagement to a task, attention spans, and interests. We observed several ways that children engaged and disengaged with their partners, such as leaving their partner and moving to another center or ignoring partner requests to engage in a task. This behavior is natural when using peer-based learning with young children who are still developing their social skills and their ability to self-regulate (Arreguín-Anderson & Alanís 2019).

Children come to a learning situation with varying levels of social development. Some children are very capable of compromising, taking turns, and listening to a partner while others are still developing these skills. Pairing children heterogeneously based on social skills, language, and/or cognitive ability creates a natural zone of proximal development for children. This zone is not static but dynamically adjusted during interactions with more knowledgeable peers while engaged in a learning task (Bedrova & Leong 2015). Intentionally pairing children based on their level of math understanding and language skills can support this development because children have to learn to negotiate their understanding of the task. This includes turn taking and sharing of materials (Alanís 2018). Interactions with others who are more socially knowledgeable improves perspective taking and collaboration. It is important for teachers to examine pair engagement levels to create a positive learning environment that supports effective partner work and children’s developing self-regulation skills.

 

 

Practical Implications

Children’s mathematical understanding is based on their levels of cognition, social and emotional development, and instructional learning environments (Moomaw 2017). Based on our research, there are several implications for early childhood teachers who are implementing partner-based learning in a variety of settings.

• Meaning making is multimodal. Young children can talk, write, draw, and dance their understanding of the world. All children must have multiple opportunities to engage in important ideas and communicate about what they are doing and why they are doing it (Kim & Kim 2017). In mathematics, there are often several ways to arrive at the same conclusion and demonstrate understanding. This idea can be fostered by encouraging multiple ways for children to share their learning while also growing their confidence as young mathematicians, including drawing, acting out, or clapping their understandings. Tapping into how children learn increases their level of participation and provides different opportunities for children to show their abilities and strengths (NAEYC 2020).
• Meaning making is most effectively internalized when it is communicated and shared with a partner. Children learn from interacting with others. Intentionally pairing children and consistently planning for paired learning are key steps in fostering cognitive, linguistic, and social development (see Arreguín-Anderson & Alanís 2019 for more information). Partners are most effective when heterogeneous pairs are formed with respect to children’s linguistic and cognitive developmental levels. When children work on tasks that have been designed to promote collaborative dialogue, they will produce language such as questioning and explaining. Social competencies should also be included. Teachers can help children develop their compromising and negotiation skills for situations when children want to stay engaged in a task longer than their partner. They can do this by providing the language children might use to negotiate conflict, designating alternating roles for turn taking, and always being realistic about what is developmentally appropriate for young children (Arreguín-Anderson & Alanís 2019).
• Interactions must be scaffolded. Young children do not arrive at our doors with the requisite skills for effective shared learning. Children benefit from sentence stems and practice to engage in quality paired learning. Early childhood educators should model interactions through their language and behavior. They can also help children by planning a learning experience, such as a game that involves these specific skills. Finally, teachers can have children role-play the sharing of materials or taking turns. As with all paired activities, gradual exposure to tasks that require collaboration and guided support by the teacher along the way will ensure successful participation.

Conclusion

We engaged in this study to determine the influence of partner-based learning on young children’s approaches to problem solving and their ability to verbalize and communicate a pattern to a partner. Our observations revealed children’s abilities to express mathematical understanding and to do so through drawing, movement, and using concrete objects. This offered children multiple entry points into the mathematical conversation and frequent opportunities to demonstrate their understanding to peers. When children are given the opportunity to learn with a partner, they can verbalize what they are learning, exchange ideas, enhance their social skills, and apply their understanding.

Partner-based learning was particularly significant in a dual language classroom where children were developing their bilingual skills and required multimodal ways of communicating and meaning making. These partner-based learning opportunities promoted active engagement and increased language input/output. Interactive and authentic classroom activities can create spaces where children can use their entire linguistic repertoire. In so doing, they enrich each other’s vocabulary, linguistic expressions, and approaches to explaining what they know.

 

 

 

---

Photographs: courtesy of the authors
Copyright © 2022 by the National Association for the Education of Young Children. See Permissions and Reprints online at NAEYC.org/resources/permissions.

References

Arreguín-Anderson, M.G., & I. Alanis. 2019. Translingual Partners in Early Childhood Elementary Education: Pedagogies on Linguistic and Cognitive Engagement. New York: Peter Lang Publishers.   

Alanis, I. 2018. “Enhancing Collaborative Learning: Activities and Structures in a Dual Language Preschool Classroom.” Association of Mexican American Educators (AMAE) Journal 12 (1): 5–26.   

Bedrova, E., & D.J. Leong. 2015. “Vygotskian and Post-Vygotskian Views on Children’s Play.” American Journal of Play 7 (3): 371–87. 

Chapin, S., & C. O’Connor. 2013. Classroom Discussions in Math: A Teachers’ Guide for  Using Talk Moves to Support the Common Core. Sausalito, CA: Math Solutions Publications.  

Fuson, K.C., D.H. Clements, & J. Sarama. 2015. “Making Early Math Education Work for All Children: Prekindergarten Teachers Lay the Foundation for Later Success in Mathematics when They Attend to the Concepts that Young Children Can and Should Learn.” Phi Delta Kappan 97 (3): 63. 

Gkloumpou, A., & D. Germanos. 2022. “The Importance of Classroom Cooperative Learning Space as an Immediate Environment for Educational Success. An Action Research Study in Greek Kindergartens.” Educational Action Research 30 (1): 61–75.     

Kibbe, M.M. & L. Feigenson. 2017. “A Dissociation Between Small and Large Numbers in Young Children’s Ability to ‘Solve for X’ in Non-Symbolic Math Problems.” Cognition 160: 82–90. 

Kim, K., & K. Kim. 2017. “Multimodal Play Literacy: A Preschooler’s Storytelling, Drawing, and Performing of Dinosaur Extinction Theories.” Early Child Development and Care 187 (3–4): 568–582. 

Moomaw, S. 2017. “Not all Preschool Math Games are Created Equal.” Young Children 72 (3): 14–20. 

NAEYC (National Association for the Education of Young Children). 2020. “Developmentally Appropriate Practice.” Position Statement. Washington, DC: NAEYC. 

Park, J., & J. Lee. 2015. “Dyadic Collaboration Among Preschool-Age Children and the Benefits of Working with a More Socially Advanced Peer.” Early Education and Development 26 (4): 574–593. 

Reed, K.E., & J. Mercer Young. 2017. “Play Games, Learn Math! Playing with Patterns.” Teaching Young Children 11 (2): 18–22. 

Spreckelsen, M., E. Dove, I. Coolen, A. Mills, A. Dowker, K. Sylva, D. Ansari, R. Merkley, V. Murphy, & G. Scerif. 2019. “Let’s Talk About Maths: The Role of Observed ‘Maths‐Talk’ and Maths Provisions in Preschoolers’ Numeracy.” Mind, Brain & Education 13 (4): 326–340.  

Vygotsky, L.S. 1978. Mind in Society: The Development of Higher Psychological Processes.  M. Cole, V. John-Steiner, S. Scribner, & E. Souberman, eds. Cambridge, MA: Harvard University Press. 

Wijns, N., L. Verschaffel, B. De Smedt, L. De Keyser, & J. Torbeyns. 2021. “Stimulating Preschoolers’ Focus on Structure in Repeating and Growing Patterns.” Learning & Instruction 74.  

Zippert, E.L., A.-A. Douglas, & B. Rittle-Johnson. 2020. “Finding Patterns in Objects and Numbers: Repeating Patterning in Pre-K Predicts Kindergarten Mathematics Knowledge.” Journal of Experimental Child Psychology 200.  

Zippert, E.L., S.H. Eason, S. Marshall, & G.B. Ramani. 2019. “Preschool Children’s Math Exploration During Play with Peers.” Journal of Applied Developmental Psychology 65.